例如传递一批货物,有不同的路径可以走,但是每条路上有传递货物数量的上限,那么在整个网络中如何能同时传递最多的货物,这样的问题称为 最大流问题 。
一、定义
流网络
流网络是一个有向图,且具有以下性质:
- 每条边都有一个 非负 的容量值 \(c(u,v)\)
- 如果存在一条边(u, v),那么 不存在 反向的边(v, u)
- 图中有两个特殊节点,源结点(source)和 汇点(sink)
流
流 \(f\) 是一个 \(V \times V \rightarrow R\) 的函数,反应的是每条边当前传递的量。有如下两个条件约束
- 容量限制:\(\forall u, v \in V, 0 \le f(u,v) \le c(u,v)\),即每条边传递量要小于边的容量
- 流量守恒:\(\forall u \in V - \{s,t\}, \sum_{v \in V} f(v,u) = \sum_{v \in V} f(u,v)\),即除源结点和汇点,流入等于流出
另外,对于流 \(\vert f \vert\) 定义为:
\[\vert f \vert = \sum_{v \in V} f(s,v) - \sum_{v \in V} f(v, s)\]即流出源结点的流量减去流入的流量。对于流网络来说,后者为 0 ,但对于之后讨论的残存网络中需要用到这一项。
对于最大流问题,我们的目标就是从源结点 s 到汇点 t ,\(\vert f \vert\) 值最大的流。
二、特殊情况处理
这些特殊情况在现实生活中经常发生,但是为了使算法保持简单,对于流网络添加了约束,使得这些特殊情况需要稍加处理。
反向边
实际生活中完全可能存在两个结点间可以互相传送的情况,很自然我们会使其变为具有反平行边的网络,然而与流网络的要求冲突。
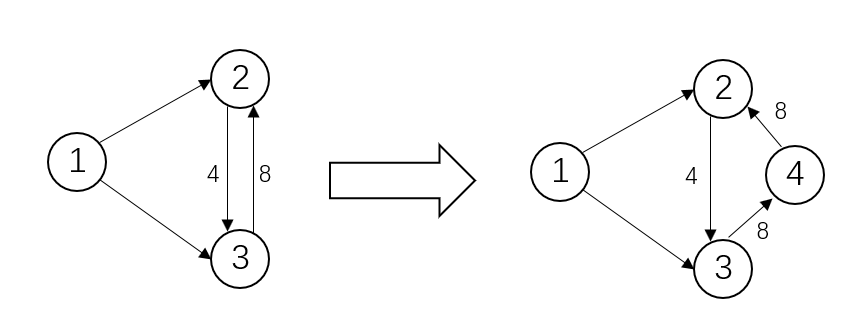
这种情况下可以通过如上处理,添加一个结点以模拟其中一条流,保证与原来网络等价的同时符合流网络的要求。
多源结点 & 多汇点
流网络中只允许一个源结点和一个汇点的存在,但是比如说传递货物,很可能具有多个工厂和多个客户,那么就会导致多个源结点和汇点的存在。
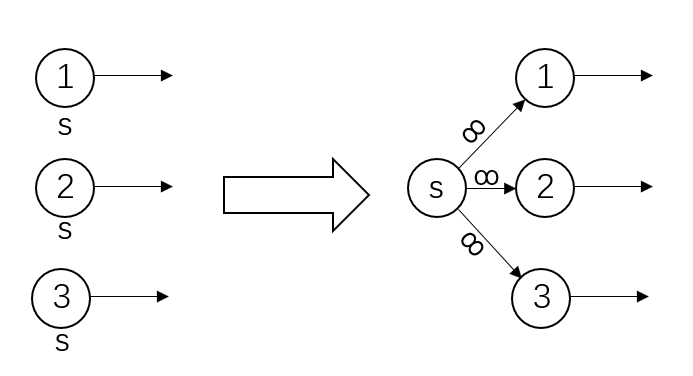
这种情况可以用一个超级源结点来连接原有的数个源结点,并且不限制之间的流量。汇点也可以用同样的方法。
三、相关概念
残存网络
残存网络(Residual Network)与原来的流网络图相同,但是原来的容量用还可以承载的量代替。例如,原本一条边容量为10,即可以传送10个单位,现在已传送7个单位,那么还可以承载 10-7 = 3 个单位,则在残存网络中记录为 3 。
另外,算法中可能需要对某条边传递的量进行缩减,为了表示这点,对于边(u, v),在残存网络中加入边(v, u),并使其值为当前已传送的量,以表示可以缩减的量,即多少正向流量能够被抵消。
因此,对于残存容量 \(c_f (u, v)\) 定义为:
\[c_f (u, v) = \begin{cases} c(u, v) - f(u, v), & (u, v) \in E \\ f(v, u), & (v, u) \in E \\ 0 & 其他 \end{cases}\]其中 \(c(u, v)\) 表示容量,\(f(u, v)\) 表示当前已使用的容量。
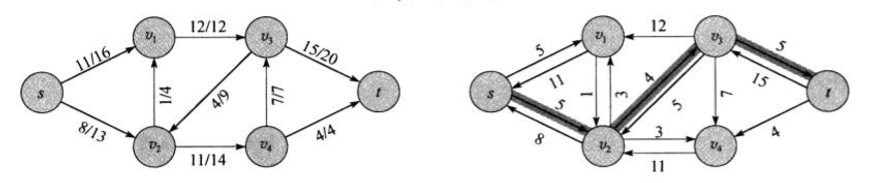
上图为一个流网络及其残存网络(引用自算法导论)。
增广路径
增广路径指的是在残存网络中从源结点到汇点的一条简单路径,如上图右侧中加深的一条。
显然,增广路径中能够提供给流网络的流量为路径上的最小值,即对于一条增广路径 p ,能够为其中每条边增加的流量的最大值为路径 p 的 残存容量,定义为:
\[c_f (p) = min \{c_f(u,v)\} , (u,v) \in p\]如上图中,路径中流量分别为 5、4、5,因此残存容量为 4 。
流网络的切割
对于一个流网络 \(G=(V,E)\),一个切割 \((S,T)\) 可以将集合 \(V\) 分为 \(S\) 和 \(T=V-S\) 两个集合。
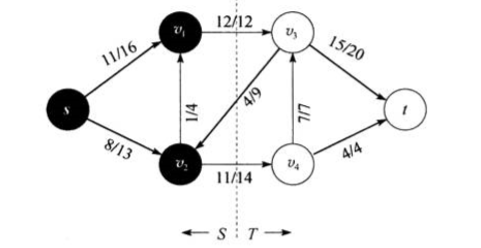
对于这样的切割,定义横跨 \((S,T)\) 的净流量为:
\[f(S,T) = \sum_{u \in S} \sum_{v \in T} f(u,v) - \sum_{u \in S} \sum_{v \in T} f(v,u)\]即从 \(S\) 流向 \(T\) 的流量之和减去流回来的流量。而容量定义为:
\[c(S,T) = \sum_{u \in S} \sum_{v \in T} c(u,v)\]一个网络中的 最小切割为整个网络中容量最小的切割 。
因此对于上图,净流量为 12 + 11 - 4 = 19 ,容量为 12 + 14 = 26 。
对于切割有如下相关性质:
- 设 \((S,T)\) 为流网络的任意切割,那么净流量 \(f(S,T) = \vert f\vert\)
- 流网络 \(G\) 中任意流 \(f\) 的值不超过 \(G\) 的任意切割的容量
- 如下几个条件等价:
- \(f\) 是 \(G\) 的一个最大流
- 残存网络中不含任何增广路径
- \(\vert f \vert = c(S,T)\),其中 \((S,T)\)为某个切割
综上可以得到,最大流的值即为最小切割的容量。
四、Ford-Fulkerson 算法
对于残存网络来说,如果其中还有增广路径,说明流依旧可以增大,该算法正是利用这一点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
ford_fulkerson(G,s,t){
for(edge(u,v) in G.E){
(u,v).f = 0
}
while(残存网络中存在增广路径 p){
for(edge(u,v) in p){
if((u,v) 存在){
(u,v).f = (u,v).f + c_f(p) //c_f(p) 为 p 的残存容量
}else{
(v,u).f = (v,u).f - c_f(p)
}
}
}
}
初始化之后,则不断寻找增广路径,如何利用残存容量对流进行更新。如果是条正向边就加上残存容量,否则缩减,直到不存在增广路径。
对于该算法,效率取决于如何寻找增广路径。如果实现流网络的数据结构合理,利用 DFS 或 BFS 找到一条路径的时间为 \(O(E)\) 。对于 while 循环来说,至多循环\(\vert f \vert\) 次,这种情况下每次循环减少一个单位,如果容量为有理数可以乘以一个系数使其均为整数。因此,总运行时间为 \(O(E \vert f \vert )\) 。
图自算法导论
Gif 根据visugo.net 制作